今天我們來做大家比較害怕的DP問題，我個人做下來發現有幾個步驟可以放我們去比較簡易的解決一個DP問題，大雞可以參考看看。

1. 看看在最一開始你能做甚麼？
2. 有沒有Base Case？
3. 做完Step1後問題變成甚麼？
4. 看看每一次遞迴之間的「關係」是甚麼？
5. 把中間狀態儲存起來
   通常有看到Maxinum或是Minium的問題「大部分」有可能是DP問題，這邊我說「大部分」就是因為，不希望大家被Maxinum跟Minium的關鍵字綁架了。

範例1-Climbing Stairs

先我們先看第一題，這題超級經典。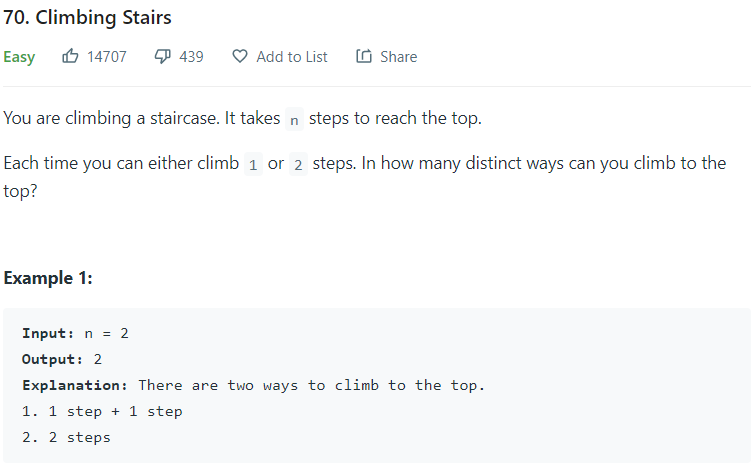

我們來想看看一開始我能做甚麼？很明顯一開始我能選擇走一步或兩步對吧。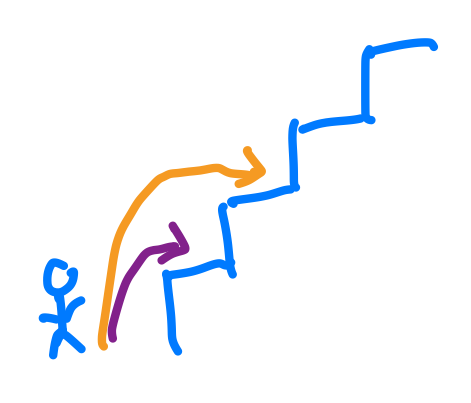

在來我們看看，有沒有Base Case？這時候我們可以用更簡單的例子來看，譬如說，n=1的時候很明顯只有一個走法，n=2有兩個走法。所以說這邊我們也輕易地找到Base Case了。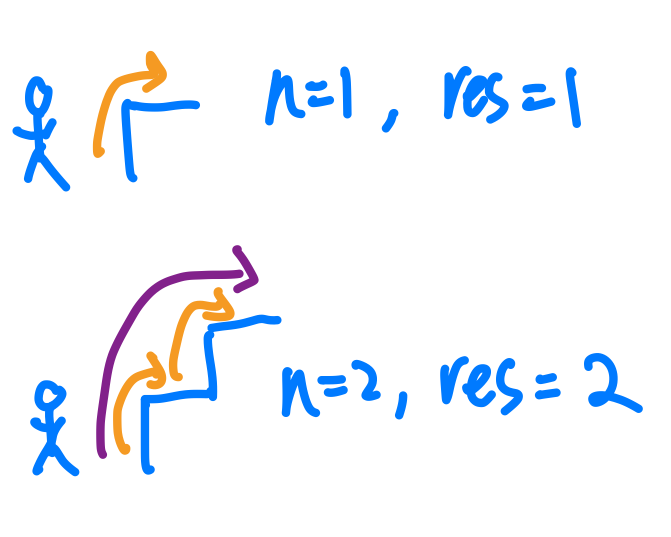

接下來我們以n=3為例，我們會發現我可以走一步或兩步，那我走一步後我們會發現，疑~這不就是n=2的問題了嗎？
我們在看走兩步的話呢？我們會發現，哇~就變成n=1的問題了。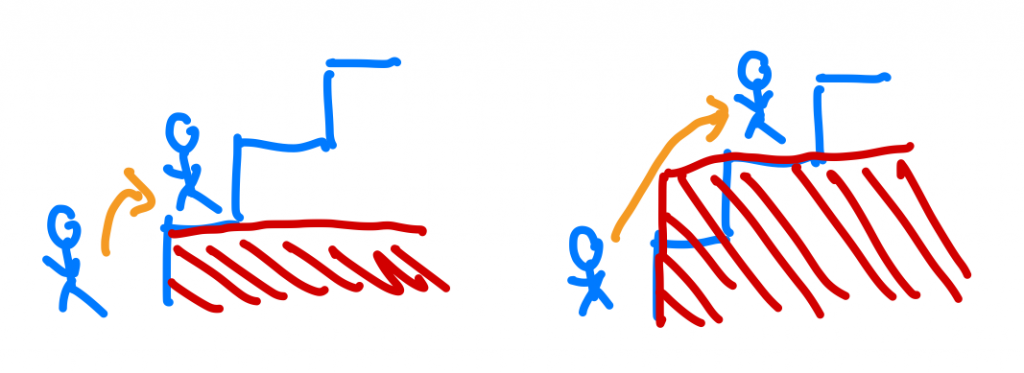

所以我們可以說，n=3的問題等於n=2加上n=1的問題，這邊就有一點感覺了，那是不是f(n) = f(n-1)+f(n-2)。接下來我們用n=4來驗證看看。我們會發現n=4也會變成n=3加上n=2的問題。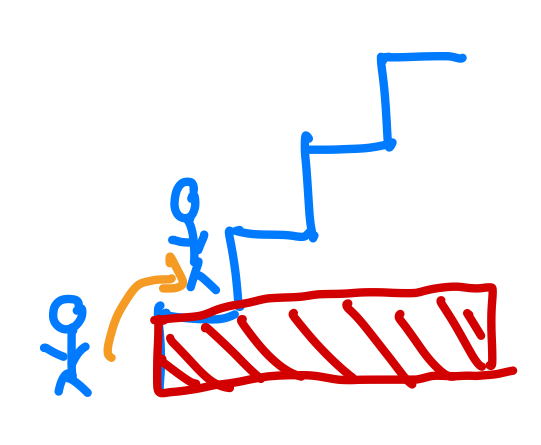

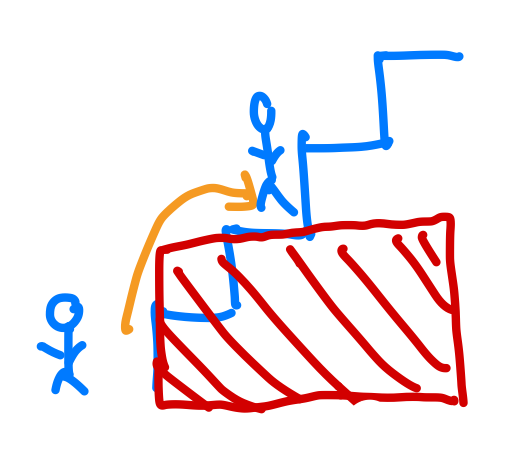
這邊我們會發現其實我們的解答已經出來了！我們來分析一下時間複雜度，有沒有發現這個跟我們當初介紹斐波那契數列一樣，所以時間複雜度是O(2^n)。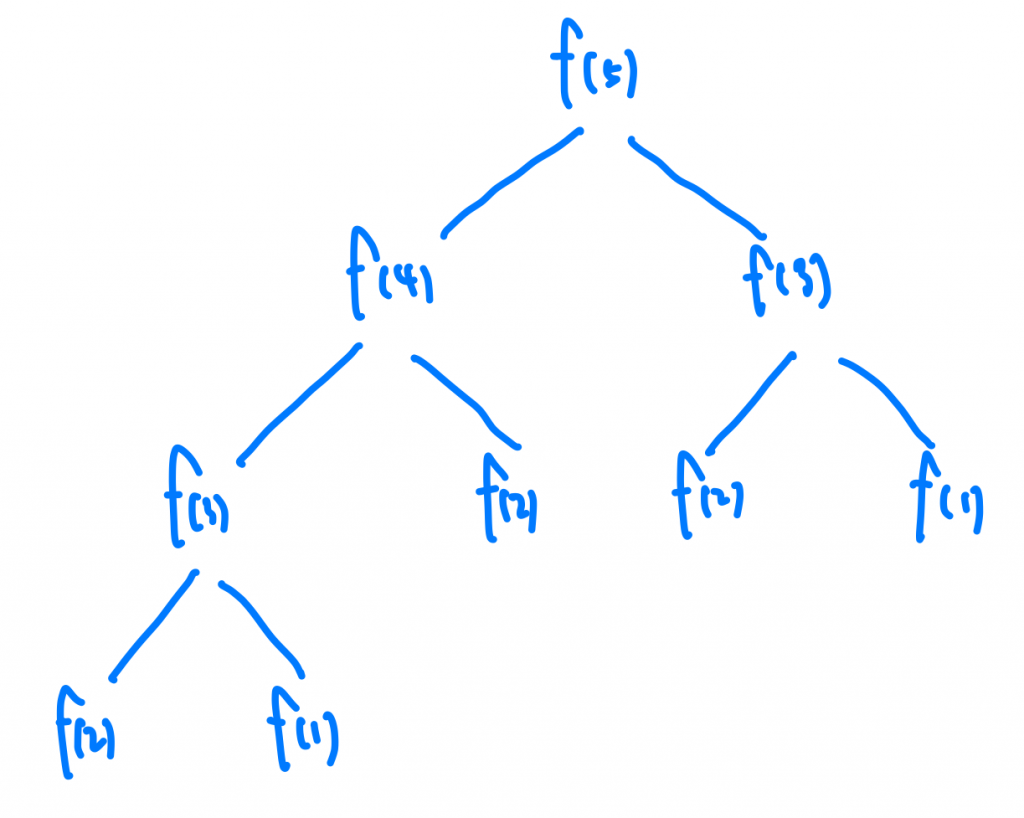

這時候我們就可以把中間的狀態記錄下來，去避免重複計算來降低我的時間複雜度，這樣就會降低成O(n)囉。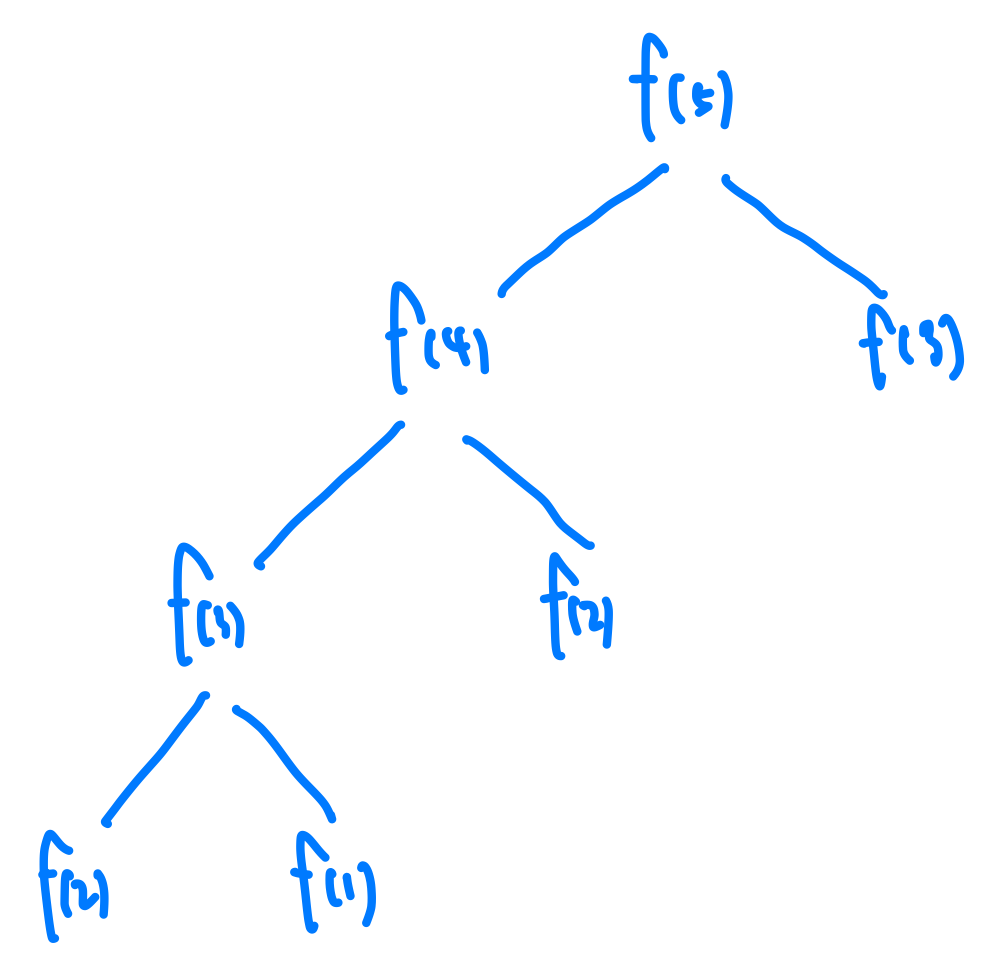

class Solution:
    
    def climbStairs(self, n: int) -> int:
        
        memo = {}
        memo[1] = 1
        memo[2] = 2
        
        def helper(n):
       
            if n in memo:
                return memo[n]
            
            res = helper(n-1) + helper(n-2)
            
            memo[n] = res
            return memo[n]
        
        return helper(n)

範例2-Coin Change

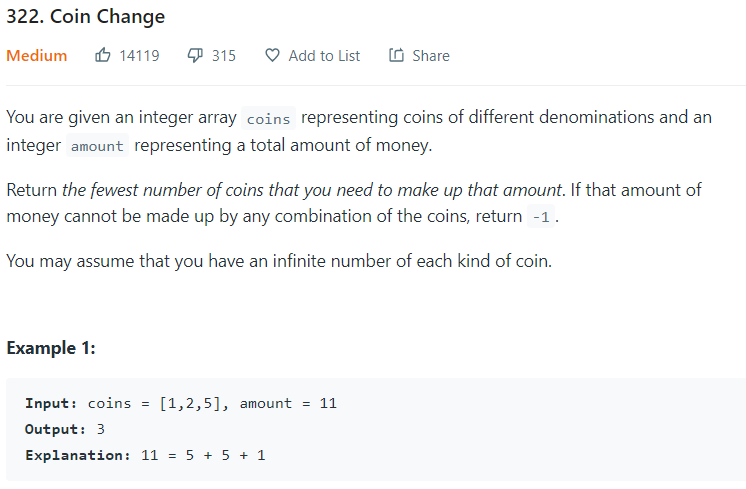
接下來我們來看這題比較有趣的，一開始看到的時候，應該會想說我就用最大的幣值去換就好啦~這就是所謂的Greedy思想。

當我們這樣做後會發現，這種情況會有問題，因為最少的應該是3+4兩個硬幣就解決而不是5+1+1總共三個硬幣。

這時候可以想看看我能做甚麼？一樣照著我上面的步驟來看一開始我可以做甚麼，很簡單的是我可以選擇任何的幣額，我們以一開始選1塊錢為例，我們會發現，這個問題變成了6塊錢的問題，如果我選3塊錢，這個問題變成了4塊錢的問題。當然其他幣額也是一樣。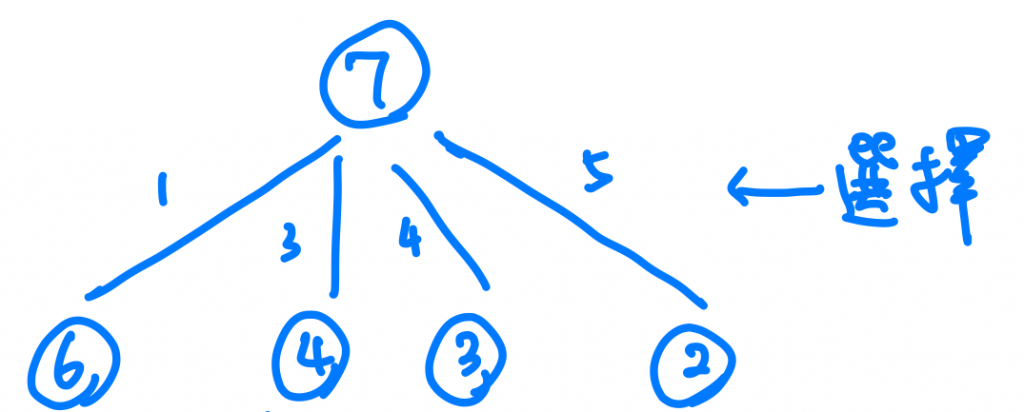

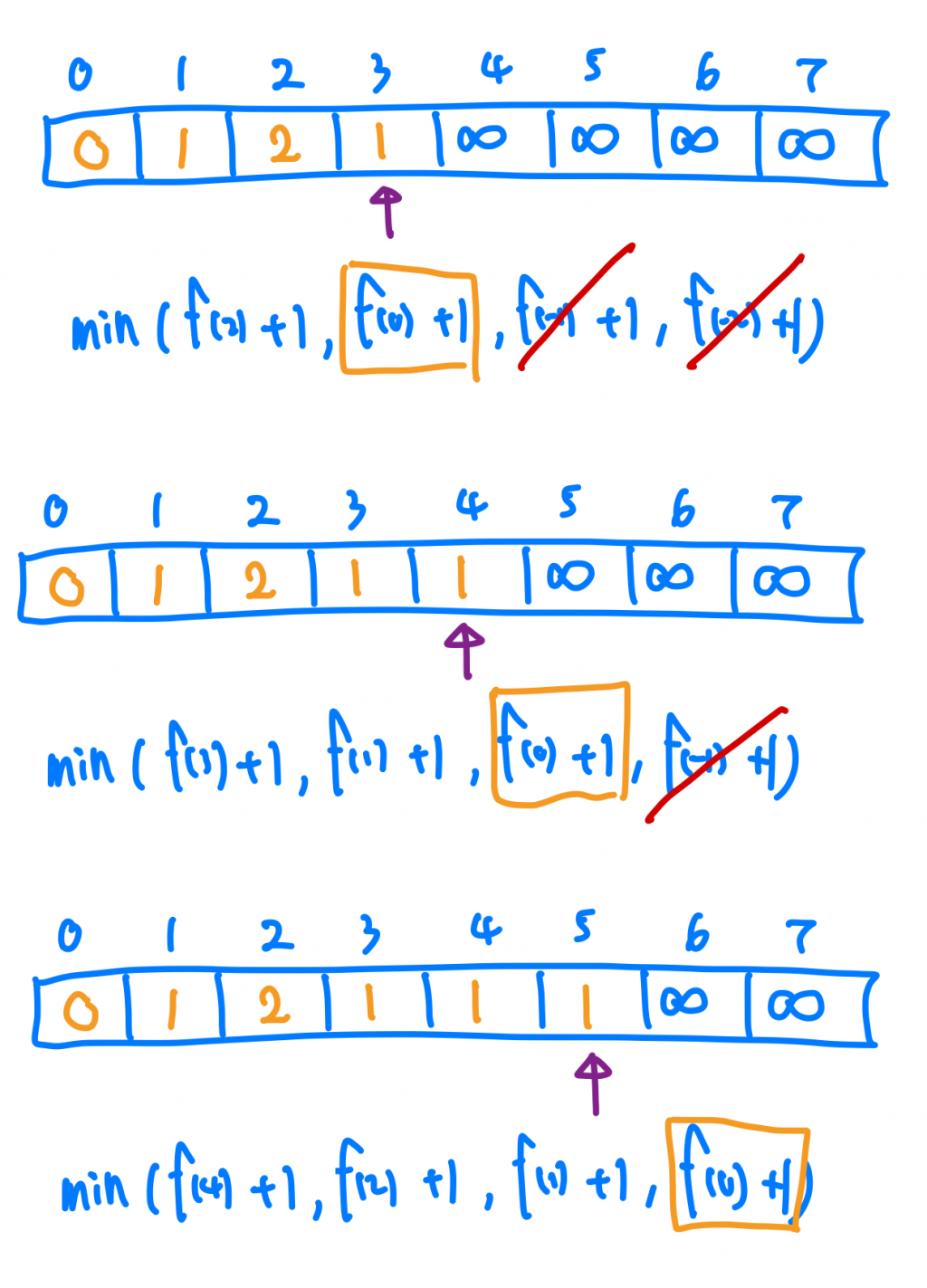
所以說以上我們可以推倒一個公式 f(n) = min(f(n-1)+1, f(n-3)+1, f(n-4)+1, f(n-5)+1)。

當我們把圖畫出來的時候會發現，其實我們會重複計算很多次一樣幣額的情況，這邊我們也是可以用DP的思想，把計算過的記錄下來，另外要注意的是，這題要求的是最少需要「幾個」硬幣，這個硬幣數量我們可以在圖上發現其實就是我們樹的高度，而Base Case就是剛好等於0的情況囉。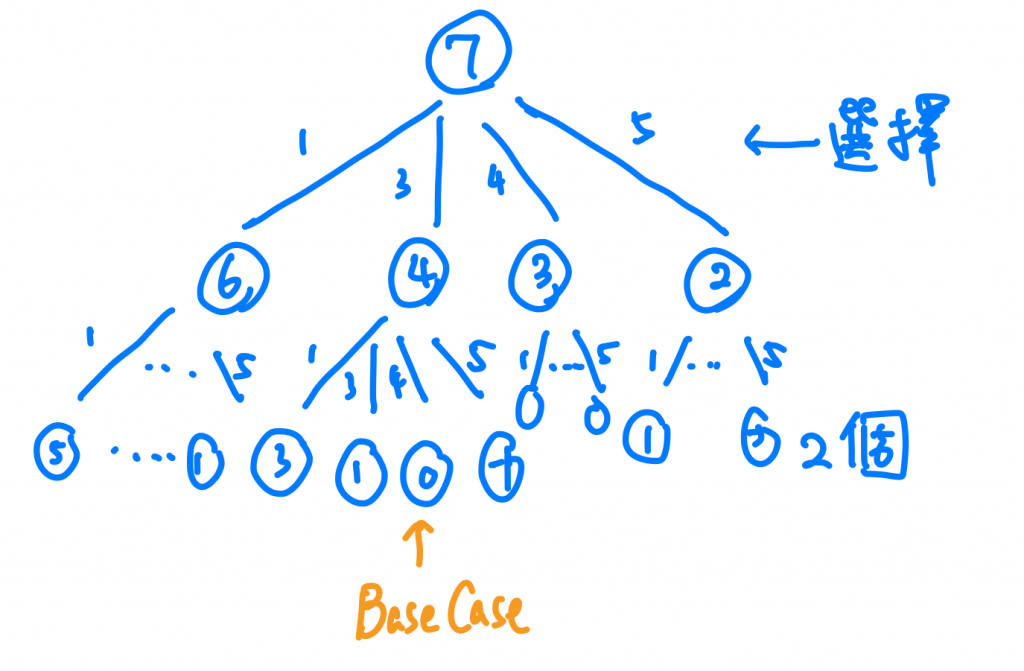

這一題我們來試看看用Bottom up的方法來做，思想上是一樣的，最重要還是我們剛剛所推導出來的公式！

首先我們先宣告一個長度amount+1的Array，我的index代表的是「在amount是index值的時候，最少需要幾個硬幣」，接著我把index 0的位置填上 0，然後開始從index 1往後走，套上剛剛的思想，去找到每一個幣額最少需要的硬幣數量(負號就不用管它了)，這樣當我們走到最後一個index答案也就出來囉！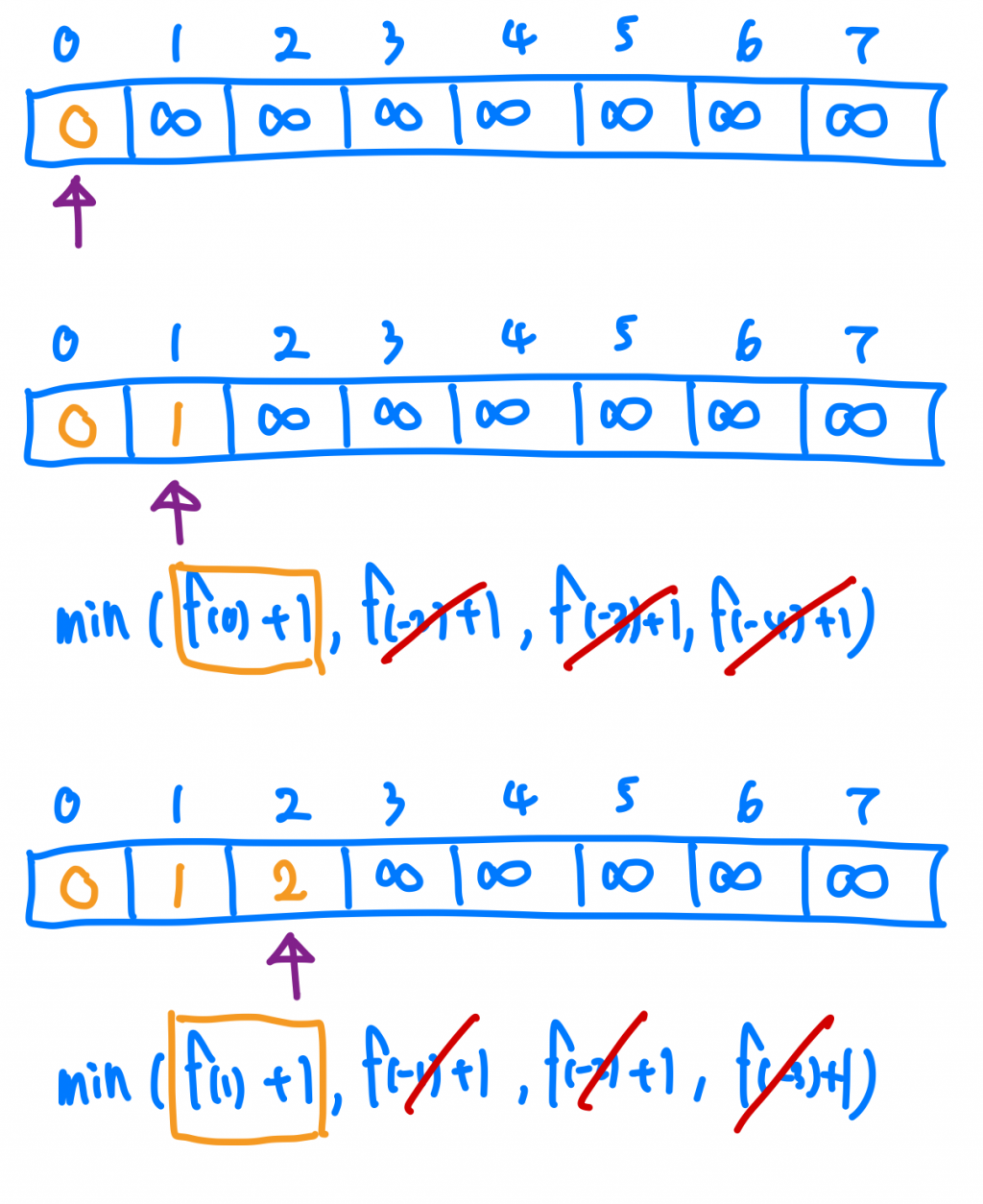

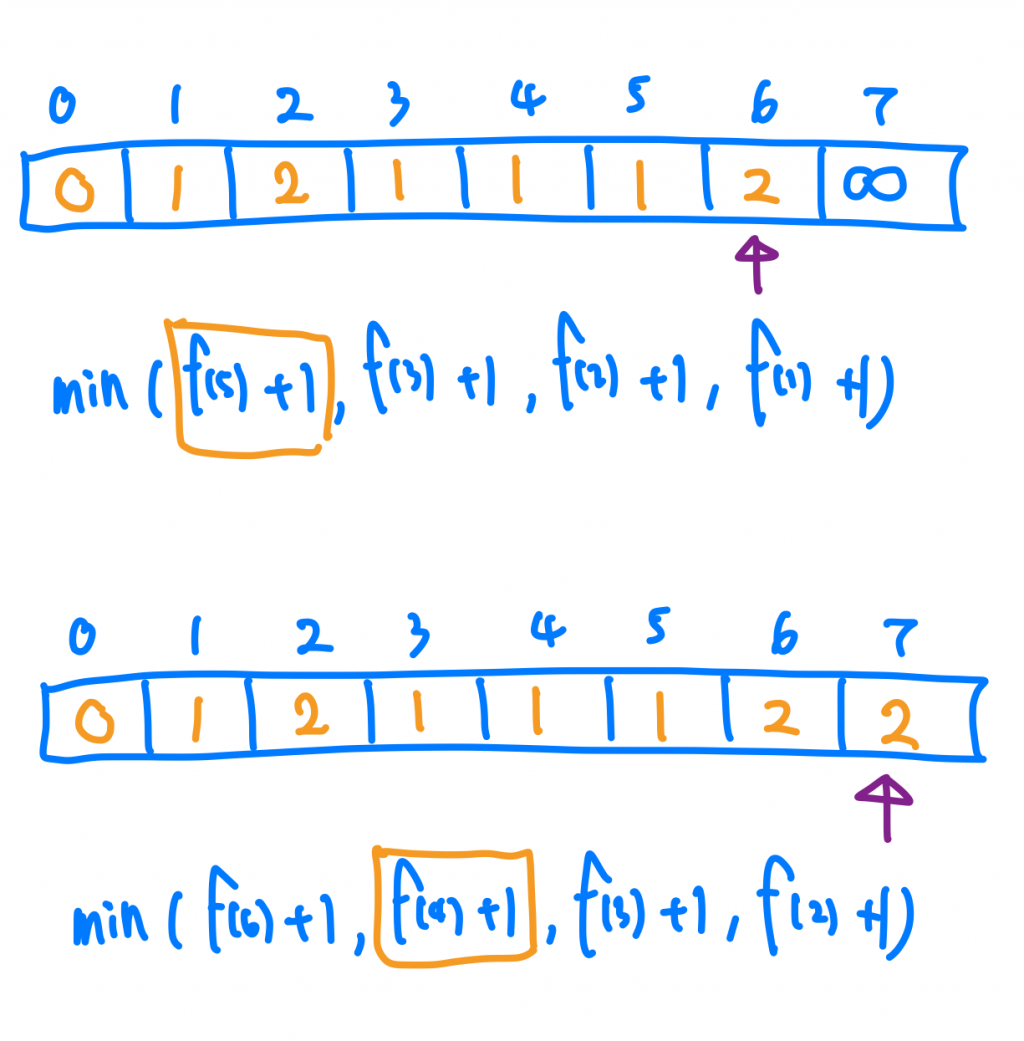
時間複雜度因為我們去走遍整個Array，而每一個index我們跑了for迴圈len(coins)次去比較最小值，所以時間複雜度就是O(nm)，n是amounts，m是len(coins)。

 class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [math.inf]*(amount+1)
        dp[0] = 0
        
        for i in range(1, amount+1):
            for c in coins:
                if i - c >= 0:
                    dp[i] = min(dp[i], dp[i-c] + 1)
        if dp[-1] != math.inf:
            return dp[amount]
        else:
            return -1